skylark::nla Namespace Reference

Classes
struct	iter_params_t
struct	iter_solver_op_t< SpParMat< IndexType, ValueType, SpDCCols< IndexType, ValueType > >, FullyDistMultiVec< IndexType, ValueType > >
struct	precond_t
struct	id_precond_t
struct	mat_precond_t
struct	tri_inverse_precond_t
struct	rand_svd_params_t
struct	randsvd_t
struct	sketched_svd_t
Functions
template<typename MatrixType , typename RhsType , typename SolType >
void	ChebyshevLS (const MatrixType &A, const RhsType &B, SolType &X, double sigma_L, double sigma_U, iter_params_t params=iter_params_t(), const precond_t< SolType > &P=id_precond_t< SolType >())
template<typename MatrixType , typename RhsType , typename SolType >
int	LSQR (const MatrixType &A, const RhsType &B, SolType &X, iter_params_t params=iter_params_t(), const precond_t< SolType > &R=id_precond_t< SolType >())
template<typename T >
void	ApproximateLeastSquares (elem::Orientation orientation, const elem::Matrix< T > &A, const elem::Matrix< T > &B, elem::Matrix< T > &X, base::context_t &context, int sketch_size=-1)
template<typename T , elem::Distribution CA, elem::Distribution RA, elem::Distribution CB, elem::Distribution RB, elem::Distribution CX, elem::Distribution RX>
void	ApproximateLeastSquares (elem::Orientation orientation, const elem::DistMatrix< T, CA, RA > &A, const elem::DistMatrix< T, CB, RB > &B, elem::DistMatrix< T, CX, RX > &X, base::context_t &context, int sketch_size=-1)
template<typename AT , typename BT , typename XT >
void	FastLeastSquares (elem::Orientation orientation, const AT &A, const BT &B, XT &X, base::context_t &context)

---

Function Documentation

template<typename T >

void skylark::nla::ApproximateLeastSquares	(	elem::Orientation	orientation,
		const elem::Matrix< T > &	A,
		const elem::Matrix< T > &	B,
		elem::Matrix< T > &	X,
		base::context_t &	context,
		int	sketch_size = -1
	)

Definition at line 11 of file least_squares.hpp.

References skylark::base::Height(), SKYLARK_THROW_EXCEPTION, and skylark::base::Width().

Referenced by main().

Here is the call graph for this function:

template<typename T , elem::Distribution CA, elem::Distribution RA, elem::Distribution CB, elem::Distribution RB, elem::Distribution CX, elem::Distribution RX>

void skylark::nla::ApproximateLeastSquares	(	elem::Orientation	orientation,
		const elem::DistMatrix< T, CA, RA > &	A,
		const elem::DistMatrix< T, CB, RB > &	B,
		elem::DistMatrix< T, CX, RX > &	X,
		base::context_t &	context,
		int	sketch_size = -1
	)

Definition at line 44 of file least_squares.hpp.

References skylark::base::Height(), SKYLARK_THROW_EXCEPTION, and skylark::base::Width().

Here is the call graph for this function:

template<typename MatrixType , typename RhsType , typename SolType >

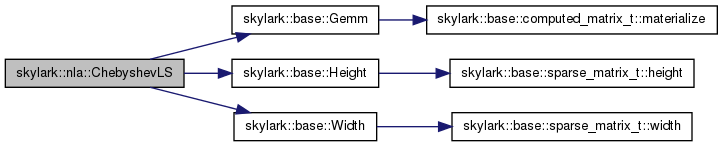
void skylark::nla::ChebyshevLS	(	const MatrixType &	A,
		const RhsType &	B,
		SolType &	X,
		double	sigma_L,
		double	sigma_U,
		iter_params_t	params = iter_params_t(),
		const precond_t< SolType > &	P = id_precond_t<SolType>()
	)

Chebyshev Semi-Iterative method.

X should be allocated, but we zero it on start. (not set as X_0).

Throughout, we will use m, n, k to denote the problem dimensions

Set the parameter values accordingly

Definition at line 23 of file Chebyshev.hpp.

References skylark::base::Gemm(), skylark::base::Height(), m, n, and skylark::base::Width().

Referenced by skylark::algorithms::accelerated_regression_solver_t< regression_problem_t< elem::DistMatrix< ValueType, VD, elem::STAR >, linear_tag, l2_tag, no_reg_tag >, elem::DistMatrix< ValueType, VD, elem::STAR >, elem::DistMatrix< ValueType, elem::STAR, elem::STAR >, lsrn_tag< PrecondTag > >::solve().

Here is the call graph for this function:

template<typename AT , typename BT , typename XT >

void skylark::nla::FastLeastSquares	(	elem::Orientation	orientation,
		const AT &	A,
		const BT &	B,
		XT &	X,
		base::context_t &	context
	)

Definition at line 110 of file least_squares.hpp.

References skylark::base::Height(), SKYLARK_THROW_EXCEPTION, and skylark::base::Width().

Referenced by main().

Here is the call graph for this function:

template<typename MatrixType , typename RhsType , typename SolType >

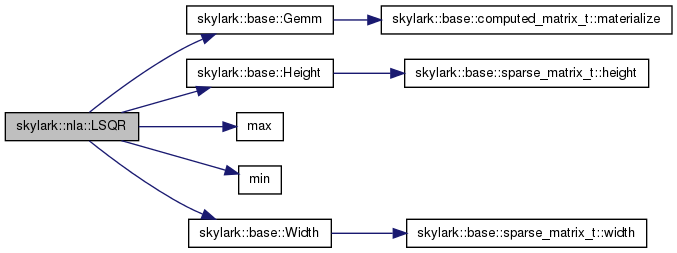
int skylark::nla::LSQR	(	const MatrixType &	A,
		const RhsType &	B,
		SolType &	X,
		iter_params_t	params = iter_params_t(),
		const precond_t< SolType > &	R = id_precond_t<SolType>()
	)

LSQR method.

X should be allocated, but we zero it on start. (not set as X_0).

Throughout, we will use m, n, k to denote the problem dimensions

Set the parameter values accordingly

Initialize everything

Return from here

Main iteration loop

1. Update u and beta

2. Estimate norm of A

3. Update v

4. Define some variables

5. Update X and W

6. Estimate norm(r)

7. estimate of norm(A'*r)

8. check convergence

9. estimate of cond(A)

10. check condition number

11. check stagnation

12. estimate of norm(X)

Definition at line 23 of file LSQR.hpp.

References skylark::base::Gemm(), skylark::base::Height(), m, max(), min(), n, and skylark::base::Width().

Referenced by skylark::algorithms::accelerated_regression_solver_t< regression_problem_t< elem::DistMatrix< ValueType, VD, elem::STAR >, linear_tag, l2_tag, no_reg_tag >, elem::DistMatrix< ValueType, VD, elem::STAR >, elem::DistMatrix< ValueType, elem::STAR, elem::STAR >, simplified_blendenpik_tag< TransformType, PrecondTag > >::solve(), skylark::algorithms::accelerated_regression_solver_t< regression_problem_t< elem::DistMatrix< ValueType, VD, elem::STAR >, linear_tag, l2_tag, no_reg_tag >, elem::DistMatrix< ValueType, VD, elem::STAR >, elem::DistMatrix< ValueType, elem::STAR, elem::STAR >, blendenpik_tag< PrecondTag > >::solve(), and skylark::algorithms::accelerated_regression_solver_t< regression_problem_t< elem::DistMatrix< ValueType, VD, elem::STAR >, linear_tag, l2_tag, no_reg_tag >, elem::DistMatrix< ValueType, VD, elem::STAR >, elem::DistMatrix< ValueType, elem::STAR, elem::STAR >, lsrn_tag< PrecondTag > >::solve().

Here is the call graph for this function: